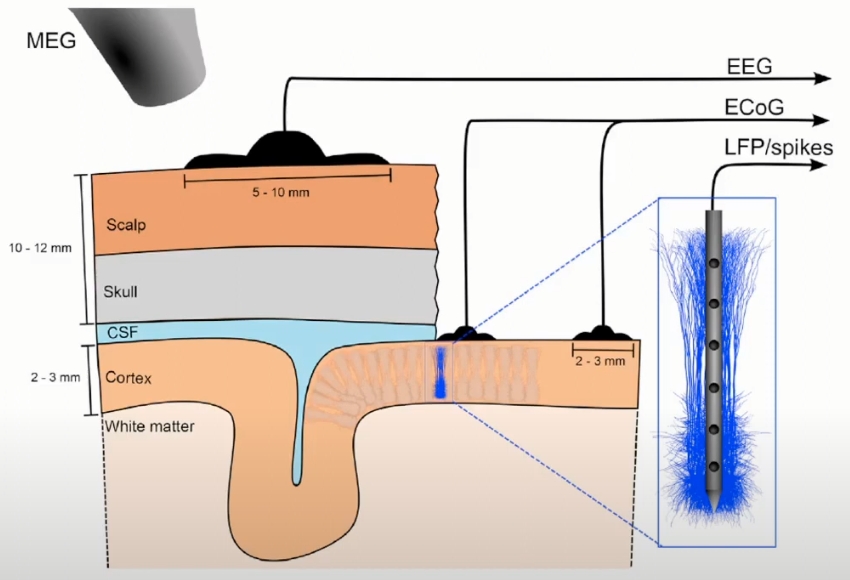
Local Field Potentials (LFPs)

Electrical Measurements of Brain Activity

Utah Array Preview Image

Low-frequency band (<300Hz): Local Filed Potential (LFP)

• Represents summed synaptic inputs from a local neuronal population (within a radius of at least a few hundred micrometers (Katzner et al., 2009; Xing et al., 2009) to over one centimeter (Kajikawa & Schroeder, 2011))

High-frequency band (>500Hz): Spikes

• Represents spiking of local neurons

• Based on subsequent processing

  1. Single-Unit Activity (SUA)
     • SUA represents the timing of spikes (i.e. action potential) fired by individual neurons.
     • Extraction: Threshold crossing + Unit classification (spike sorting).
  2. Multi-Unit Activity (MUA)/Multi-Unit Spike (MSP)
     • MSP represents all detected spikes (without spike sorting) which represent the aggregate spikes from an ensemble of neurons within a radius of 140–300 μm in the vicinity of the electrode tip.
  3. Entire Spiking Activity (ESA)
     • ESA is represented by a continuous signal and reflects an instantaneous measure of the number and size of spikes from a population of neurons around the recording electrode.
     • Extraction: Full-wave rectification (taking the absolute value + low-pass filtering).

Forward-modeling

The word “forward” denotes that the extracellular potentials are modeled from known neural sources.

The “measurement physics”, i.e., the link between neural activity and what is measured, is well-understood. The last decade has seen the refinement of a well-founded biophysical forward-modeling scheme based on volume conduction theory (Rall & Shepherd, 1968; Holt & Koch, 1999) to incorporate detailed reconstructed neuronal morphologies in precise calculations of extracellular potentials both spikes (Holt & Koch, 1999; Gold et al., 2006; Gold et al., 2007; Pettersen & Einevoll, 2008; Pettersen et al., 2008; Schomburg et al., 2012; Reimann et al., 2013) and LFPs (Einevoll et al., 2007; Pettersen et al., 2008; Lindén et al., 2010; Lindén et al., 2011; Gratiy et al., 2011; Schomburg et al., 2012; Łęski et al., 2013; Reimann et al., 2013).

Simulation Software

• NEURON (Carnevale & Hines, 2006)

• LFPy (Lindén et al., 2014)

  Existing multicompartmental neuron models, available from databases like ModelDB (Hines et al., 2004), can readily be adapted for use with the LFPy-package.

Inverse-modeling

The “inverse” problem of estimating the underlying sources from recorded potentials is relatively ill-posed.

Inferring SUA from LFP

(Hall et al., 2014)

• Methods
  • Wrist torque-controlled task
  • Low-frequency LFP (lf-LFP) (<5Hz)
  • Multiple-input, multiple-output (MIMO) module

(Rule et al., 2015)

• Methods
  • Free-Reach and Grasp (FRG)
  • Multiple frequency bands
  • Generalized linear point process model, Negative log-likelihood under L2 regularization (using gradient descent)

(Manning et al., 2009)

• Methods
  • Recordings were obtained in widespread brain regions including the frontal cortex, posterior cortex (occipital and parietal cortices), amygdala, hippocampus, and parahippocampal region
  • The primary objective was to examine how the firing rates of individual neurons related to narrowband changes (i.e., oscillations) and broadband changes in the LFP.
  • Wavelets Transform (Morlet wavelets)

Inferring MUA/MSP from LFP

(Bansal et al., 2011)

• Methods
  • Continuous grasping task
  • Low-frequency LFP (lf-LFP)
  • Savitzy Golay filter (2nd order, 0.5 s)

(Rasch et al., 2008)

• Methods
  • The primary visual cortex (V1)
  • Multiple frequency bands
  • Support Vector Machine (SVM) and standard linear regression

Inferring ESA from LFP

(Ahmadi et al., 2021)

• Methods
  • Point-to-point task and Reach-to-grasp task
  • Multiple frequency bands
  • Multivariate multiple linear regression (MLR)

Inferring Morphology (Single Neuron) from LFP

(Chen et al., 2021)

• Methods
  • Sequential Neural Posterior Estimation (Bayesian-based)
  • Better performance when extending the parameter set \((x, y, z, \phi,\lambda) \longrightarrow (x, y, z, \phi,\lambda, R_s, L_t, R_t)\)
    • Location \((x, y, z)\)
    • Orientation \((\phi, \lambda)\)
    • Soma radius \(R_s\); Trunk length \(L_t\); Trunk radius \(R_t\);
  • CNN for further improvement

Inferring Spatial Information from LFP

Cortical Column/Hypercolumn

The term “cortical column” is a complex and evolving concept, reflecting the ever-increasing understanding of the brain’s intricate structure and function. While one of the definitions, encompassing “interconnected neurons with common input, common output, and common response properties extending through the thickness of the cortex,” serves as a useful starting point for inferencing spatial locations from LFP. (Molnár & Rockland, 2020)

The Size of Hypercolumn and Minicolumn

A cortical column is a group of neurons forming a cylindrical structure through the cerebral cortex of the brain perpendicular to the cortical surface. The columnar functional organization, as originally framed by (Mountcastle, 1957), suggests that neurons that are horizontally more than 0.5 mm (500 µm) from each other do not have overlapping sensory receptive fields, and other experiments give similar results: 200–800 µm (Buxhoeveden & Casanova, 2002; Hubel et al., 1977; Leise, 1990).

A cortical minicolumn (also called cortical microcolumn) is a vertical column through the cortical layers of the brain. Minicolumns comprise perhaps 80–120 neurons, except in the Primate Primary Visual Cortex (V1), where there are typically more than twice the number. There are about \(2 \times 10^8\) minicolumns in humans (Johansson & Lansner, 2007). The diameter of a minicolumn is about 28–40 μm (Mountcastle, 1957).

Neurons within a minicolumn (microcolumn) encode similar features, whereas a hypercolumn “denotes a unit containing a full set of values for any given set of receptive field parameters” (Horton & Adams, 2005).

Assume the LFP reach is a circle of radius \(R\); hypercolumn is a point, located at the center of a hexagon of edge width \(W\), then the spacing between two hypercolumns are \(\sqrt{3}W\);

\[N_{hypercolumn} = \frac{\pi R^2}{ \frac{3\sqrt{3}}{2}W^2 } \approx 1.21 \times (\frac{R}{W})^2\]

LFP Reach (\(R (\mu m)\))	Cortical Column Spacing (\(\sqrt{3}W (\mu m)\))	\(N_{hypercolumn}\)
1000	200	90.74
1000	300	40.33
500	200	22.69
500	300	10.08

Reference

1. Ahmadi, N., Constandinou, T. G., & Bouganis, C.-S. (2021). Inferring entire spiking activity from local field potentials. Sci. Rep., 11(19045), 1–13. https://doi.org/10.1038/s41598-021-98021-9
2. Bansal, A. K., Vargas-Irwin, C. E., Truccolo, W., & Donoghue, J. P. (2011). Relationships among low-frequency local field potentials, spiking activity, and three-dimensional reach and grasp kinematics in primary motor and ventral premotor cortices. J. Neurophysiol. https://journals.physiology.org/doi/full/10.1152/jn.00532.2010
3. Buxhoeveden, D. P., & Casanova, M. F. (2002). The minicolumn hypothesis in neuroscience. Brain, 125(5), 935–951. https://doi.org/10.1093/brain/awf110
4. Carnevale, N. T., & Hines, M. L. (2006). The NEURON Book. In Cambridge Core. Cambridge University Press. https://doi.org/10.1017/CBO9780511541612
5. Chen, Z., Dopp, D., Nair, S. S., & Headley, D. B. (2021). Inferring Morphology of a Neuron from In Vivo LFP Data. In 2021 10th International IEEE/EMBS Conference on Neural Engineering (NER) (pp. 04–06). IEEE. https://doi.org/10.1109/NER49283.2021.9441161
6. Einevoll, G. T., Pettersen, K. H., Devor, A., Ulbert, I., Halgren, E., & Dale, A. M. (2007). Laminar population analysis: estimating firing rates and evoked synaptic activity from multielectrode recordings in rat barrel cortex. Journal of Neurophysiology, 97(3), 2174–2190.
7. Gold, C., Henze, D. A., & Koch, C. (2007). Using extracellular action potential recordings to constrain compartmental models. Journal of Computational Neuroscience, 23, 39–58.
8. Gold, C., Henze, D. A., Koch, C., & Buzsaki, G. (2006). On the origin of the extracellular action potential waveform: a modeling study. Journal of Neurophysiology, 95(5), 3113–3128.
9. Gratiy, S. L., Devor, A., Einevoll, G. T., & Dale, A. M. (2011). On the estimation of population-specific synaptic currents from laminar multielectrode recordings. Frontiers in Neuroinformatics, 5, 32.
10. Hall, T. M., Nazarpour, K., & Jackson, A. (2014). Real-time estimation and biofeedback of single-neuron firing rates using local field potentials. Nat. Commun., 5(5462), 1–12. https://doi.org/10.1038/ncomms6462
11. Hines, M. L., Morse, T., Migliore, M., Carnevale, N. T., & Shepherd, G. M. (2004). ModelDB: a database to support computational neuroscience. Journal of Computational Neuroscience, 17, 7–11.
12. Holt, G. R., & Koch, C. (1999). Electrical interactions via the extracellular potential near cell bodies. Journal of Computational Neuroscience, 6, 169–184.
13. Horton, J. C., & Adams, D. L. (2005). The cortical column: a structure without a function. Philosophical Transactions of the Royal Society B: Biological Sciences, 360(1456), 837. https://doi.org/10.1098/rstb.2005.1623
14. Hubel, D. H., Wiesel, T. N., & Stryker, M. P. (1977). Orientation columns in macaque monkey visual cortex demonstrated by the 2-deoxyglucose autoradiographic technique. Nature, 269, 328–330. https://doi.org/10.1038/269328a0
15. Johansson, C., & Lansner, A. (2007). Towards cortex sized artificial neural systems. Neural Networks, 20(1), 48–61. https://doi.org/10.1016/j.neunet.2006.05.029
16. Kajikawa, Y., & Schroeder, C. E. (2011). How local is the local field potential? Neuron, 72(5), 847–858.
17. Katzner, S., Nauhaus, I., Benucci, A., Bonin, V., Ringach, D. L., & Carandini, M. (2009). Local origin of field potentials in visual cortex. Neuron, 61(1), 35–41. https://doi.org/10.1016/j.neuron.2008.11.016
18. Leise, E. M. (1990). Modular construction of nervous systems: A basic principle of design for invertebrates and vertebrates. Brain Res. Rev., 15(1), 1–23. https://doi.org/10.1016/0165-0173(90)90009-D
19. Lindén, H., Hagen, E., Łęski, S., Norheim, E. S., Pettersen, K. H., & Einevoll, G. T. (2014). LFPy: a tool for biophysical simulation of extracellular potentials generated by detailed model neurons. Frontiers in Neuroinformatics, 7, 41.
20. Lindén, H., Pettersen, K. H., & Einevoll, G. T. (2010). Intrinsic dendritic filtering gives low-pass power spectra of local field potentials. Journal of Computational Neuroscience, 29, 423–444.
21. Lindén, H., Tetzlaff, T., Potjans, T. C., Pettersen, K. H., Grün, S., Diesmann, M., & Einevoll, G. T. (2011). Modeling the spatial reach of the LFP. Neuron, 72(5), 859–872.
22. Manning, J. R., Jacobs, J., Fried, I., & Kahana, M. J. (2009). Broadband Shifts in Local Field Potential Power Spectra Are Correlated with Single-Neuron Spiking in Humans. J. Neurosci., 29(43), 13613–13620. https://doi.org/10.1523/JNEUROSCI.2041-09.2009
23. Molnár, Z., & Rockland, K. S. (2020). Cortical columns. In Neural Circuit and Cognitive Development (Second Edition) (pp. 103–126). Academic Press. https://doi.org/10.1016/B978-0-12-814411-4.00005-6
24. Mountcastle, V. B. (1957). MODALITY AND TOPOGRAPHIC PROPERTIES OF SINGLE NEURONS OF CAT’S SOMATIC SENSORY CORTEX. J. Neurophysiol. https://doi.org/10.1152/jn.1957.20.4.408
25. Pettersen, K. H., & Einevoll, G. T. (2008). Amplitude variability and extracellular low-pass filtering of neuronal spikes. Biophysical Journal, 94(3), 784–802.
26. Pettersen, K. H., Hagen, E., & Einevoll, G. T. (2008). Estimation of population firing rates and current source densities from laminar electrode recordings. Journal of Computational Neuroscience, 24, 291–313.
27. Rall, W., & Shepherd, G. M. (1968). Theoretical reconstruction of field potentials and dendrodendritic synaptic interactions in olfactory bulb. Journal of Neurophysiology, 31(6), 884–915.
28. Rasch, M. J., Gretton, A., Murayama, Y., Maass, W., & Logothetis, N. K. (2008). Inferring Spike Trains From Local Field Potentials. J. Neurophysiol. https://journals.physiology.org/doi/full/10.1152/jn.00919.2007
29. Reimann, M. W., Anastassiou, C. A., Perin, R., Hill, S. L., Markram, H., & Koch, C. (2013). A biophysically detailed model of neocortical local field potentials predicts the critical role of active membrane currents. Neuron, 79(2), 375–390.
30. Rule, M. E., Vargas-Irwin, C., Donoghue, J. P., & Truccolo, W. (2015). Contribution of LFP dynamics to single-neuron spiking variability in motor cortex during movement execution. Front. Syst. Neurosci., 9, 141041. https://doi.org/10.3389/fnsys.2015.00089
31. Schomburg, E. W., Anastassiou, C. A., Buzsáki, G., & Koch, C. (2012). The spiking component of oscillatory extracellular potentials in the rat hippocampus. Journal of Neuroscience, 32(34), 11798–11811.
32. Xing, D., Yeh, C.-I., & Shapley, R. M. (2009). Spatial Spread of the Local Field Potential and its Laminar Variation in Visual Cortex. J. Neurosci., 29(37), 11540–11549. https://doi.org/10.1523/JNEUROSCI.2573-09.2009
33. Łęski, S., Lindén, H., Tetzlaff, T., Pettersen, K. H., & Einevoll, G. T. (2013). Frequency dependence of signal power and spatial reach of the local field potential. PLoS Computational Biology, 9(7), e1003137.